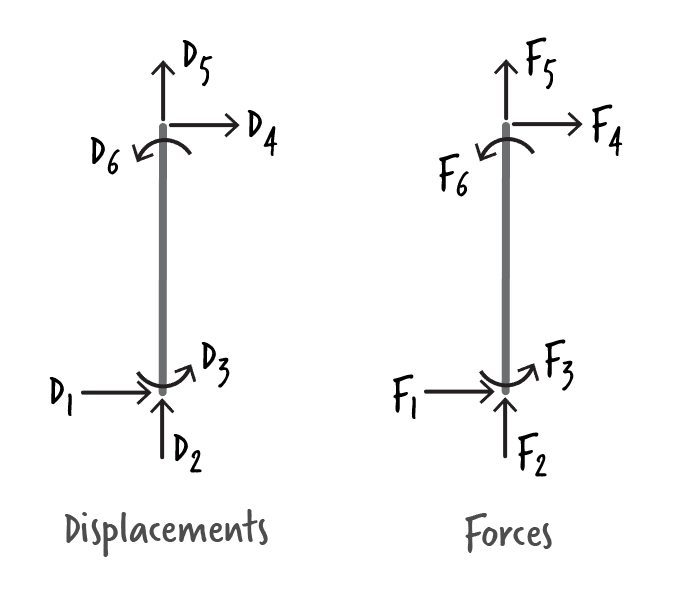
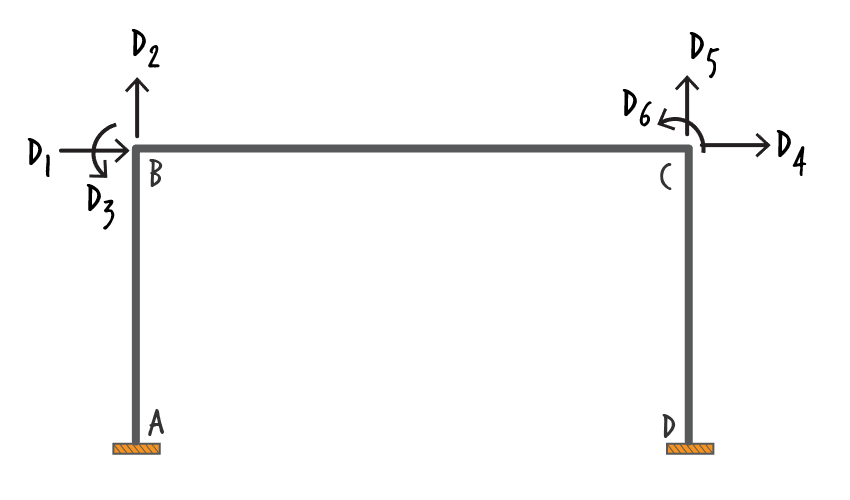
SA51: Frame Analysis Example (Matrix Displacement Method)
Problem Definition
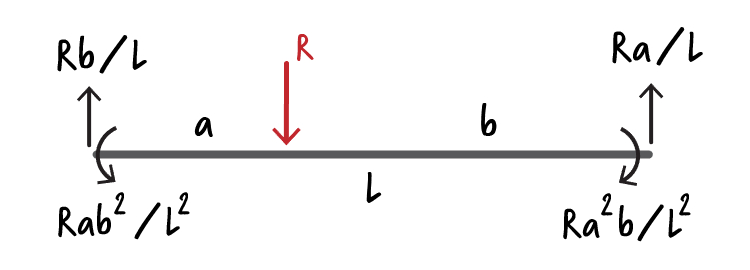
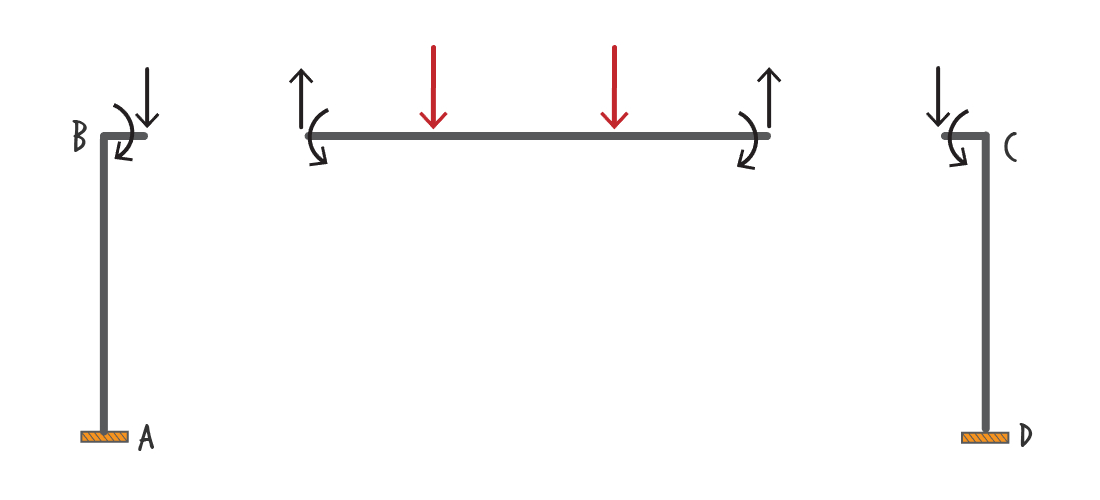
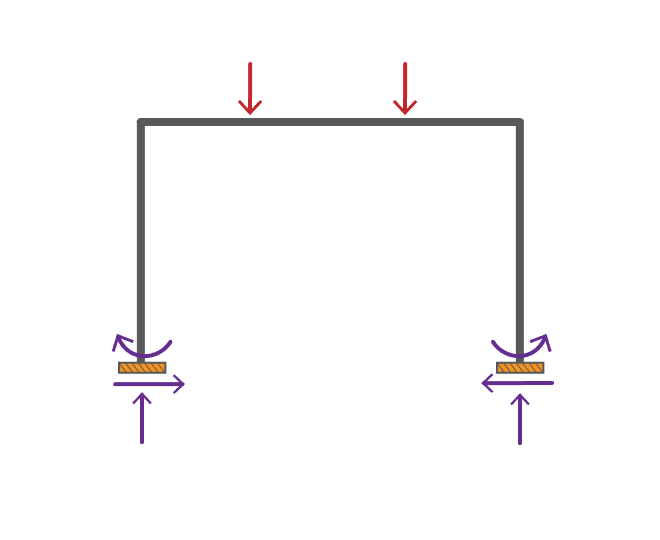
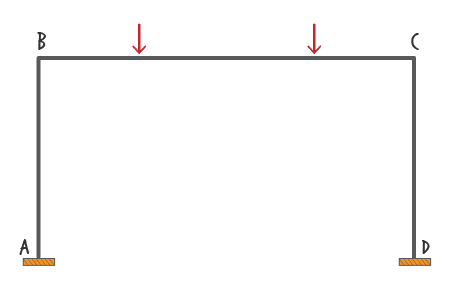
Analyze the frame shown below using the Matrix Displacement Method. The frame is subjected to two concentrated member loads. There is a concentrated load of \( \small kN \) acting on Member BC. It is located \( \small m \) to the right of joint B. The other concentrated load has a magnitude of \( \small kN\), and it is located \( \small m \) to the left of joint C. Members AB and DC each has a length of \( \small m \). The overall length of BC is \( \small m \).
The members are made of structural steel with a modulus of elasticity ( \( \small E\) ) of \( \small GPa\). Members AB and CD each has a corss-sectional area ( \(\small A\) ) of \( \small mm^2 \) and moment of inertia ( \( \small I\) ) of \( \small mm^4 \). Member BC has a cross-sectional area of \( \small mm^2 \); and a moment of inertia of \( \small mm^4 \).
Note: Move the cursor over an input field to see the valid range of values. Note: The source of this problem can be found in this video: YOUTUBE. Note: For a detail explanation of the Matrix Displacement Method, take our online course.